Função de Sobrevivência
Função de Sobrevivência
Nos estudos de sobrevivência, um dos principais interesses está na sobrevida, ou no tempo de vida adicional de um dado indivíduo. Seja \(T\) a variável aleatória positiva, que indica o tempo de vida adicional de uma pessoa qualquer . Então a função de sobrevivência corresponde a probabilidade de que essa pessoa ultrapasse um tempo pré determinado \(t\). Ou seja:
\[ S(t) = P(T > t) \]
Em contrapartida o complementar a função sobrevivência é a função
acumulada, que nesse contexto indica a probabilidade que a morte ocorra
antes de \(t\) , ou seja, \(F(t) = 1 − S(t)\).
Como exemplo em um estudo médico onde o evento de interesse é a
morte, a função de sobrevivência fornece a probabilidade de um indivíduo
de idade \(x\) sobreviver a \(x+t\).
A função de sobrevivência é uma função não crescente tal que \(S(0)=1\) e \(\lim_{t\rightarrow \infty} S(t)=0\). A notação utilizada para função de sobrevivência é variada, aparecendo na litaratura como \(S(t)\) , \(\bar{F}(t)\) ou \(_xp_t\).
Função Sobrevivência
Considere um indivíduo recém-nascido, \(x=0\). A sobrevida, \(T_x\), é uma variável aleatória do tipo contínua, Então \(F_{T}(t)\) representa a função de distribuição de \(T\) tal que
\[ F_{T}(t) = P (T ≤ t ) \text{, }t ≥0 \] e seja
\[S(t) = 1 − F(t) = P(T > t ) \text{, } t ≥ 0 \]
Já a idade desse mesmo indivíduo após ter atingido \(x\) anos pode ser calculada por \(S_{T_x}(t)=P(T>x+t|T>x)\), assim
\[ S_{T_x}(t)=P(T>x+t|T>x)=\frac{S(t+x)}{S(x)} \]
Abaixo um exemplo de função de sobrevivência moldando uma coorte hipotética de 100.000 indivíduos através das probabilidades de sobrevivência e morte da população brasileira para 4 anos distindos (1998, 2004,2008 e 2012).
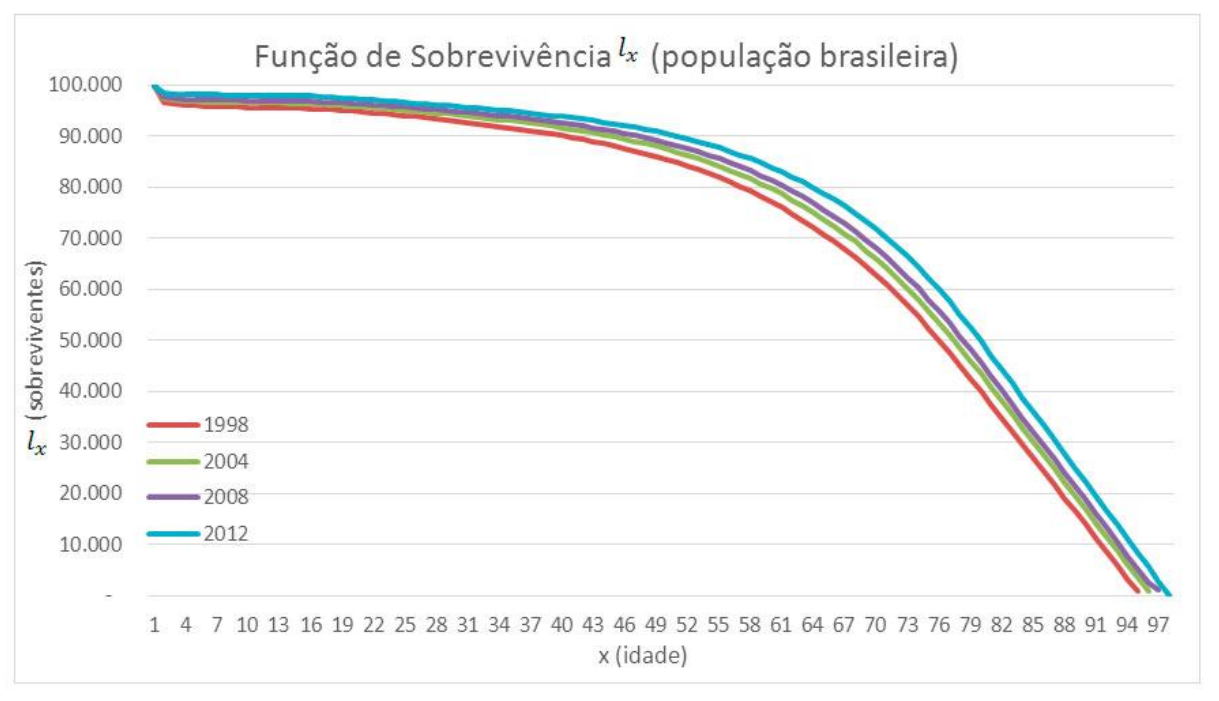
Observe que a função se inicia num determinado momento no tempo, com 100% da população ainda viva e com saúde e nos permite calcular qual a porcentagem dessa população ainda viva e com saúde noutros momentos ao longo do tempo.
A função de sobrevivência pode ser feita através da tábua de vida, tomaremos como exemplo 5 anos de uma coorte hipotética de 100000 habitantes cuja probabilidade de morte é dada por $n q_x=F{T_x}(n) $ . A função \(S_{T_x}(t)\) calcula a probabilidadede um individuo de idade \(x\) sobreviver até a idade \(x+1\).
| \(X\) | \(\text{ }_1q_x\) | \(l_x\) | \(S_{T_x}(1)\) |
|---|---|---|---|
| 0 | 0,01260 | 100000 | 1 |
| 1 | 0,00093 | 98740 | 0,9874 |
| 2 | 0,00065 | 98648 | 0,9865 |
| 3 | 0,00050 | 98584 | 0,9858 |
| 4 | 0,00040 | 98535 | 0,9854 |
| 5 | 0,00037 | 98496 | 0,9850 |
| 6 | … | … | … |
Tomemos como exemplo o segundo ano, se esperamos que \(0,00065\) da coorte morram antes de completar \(3\) anos uma vez que \(98648\) indivíduos estão vivos, calculamos: \(0,00065.98648 = 641212\) (são os indivíduos da coorte que sobreviveram até \(2\) anos mas morrem antes de completar \(3\)), \(98648 – 641212 = 98584\) (são os que chegaram vivos ao terceiro ano, sendo então \(98584/100000\) a probabilidade de um indivíduo que desta corte chegar vivo ao terceiro ano.
Referências
Este conteúdo está disponível por meio da Licença Creative Commons 4.0
LIGA DE CIÊNCIAS ATUARIAIS
CNPJ 44.515.919/0001-93
